Functional Arrays in Elixir and Erlang
Many data structures including arrays don't translate equally from imperative to functional programming languages and there are important reasons why.
Arrays are the most foundational data structure in most programming languages but many data structures including arrays don't translate equally from imperative to functional programming languages and there are important reasons why this is the case.
Unlike traditional imperative programming, where computation is a sequence of transitions from states to states, functional programming has no implicit state and places its emphasis entirely on expressions or terms with immutable values.
In an imperative setting, = refers to a destructive update, assigning a new value to the left-hand-side variable, whereas in a functional setting = means true equality: x is equal to 1 in any execution context.
This characteristic of functional programming (known as referential transparency or purity) has a profound influence on how programs are constructed, reasoned about and perform under certain conditions as we'll see in this section.
Subscribe to the free newsletter for updates!
Imperative Array
This is an over-simplified version of how a computer will store an array in memory intended to illustrate a few operations on arrays in imperative settings.
Storage
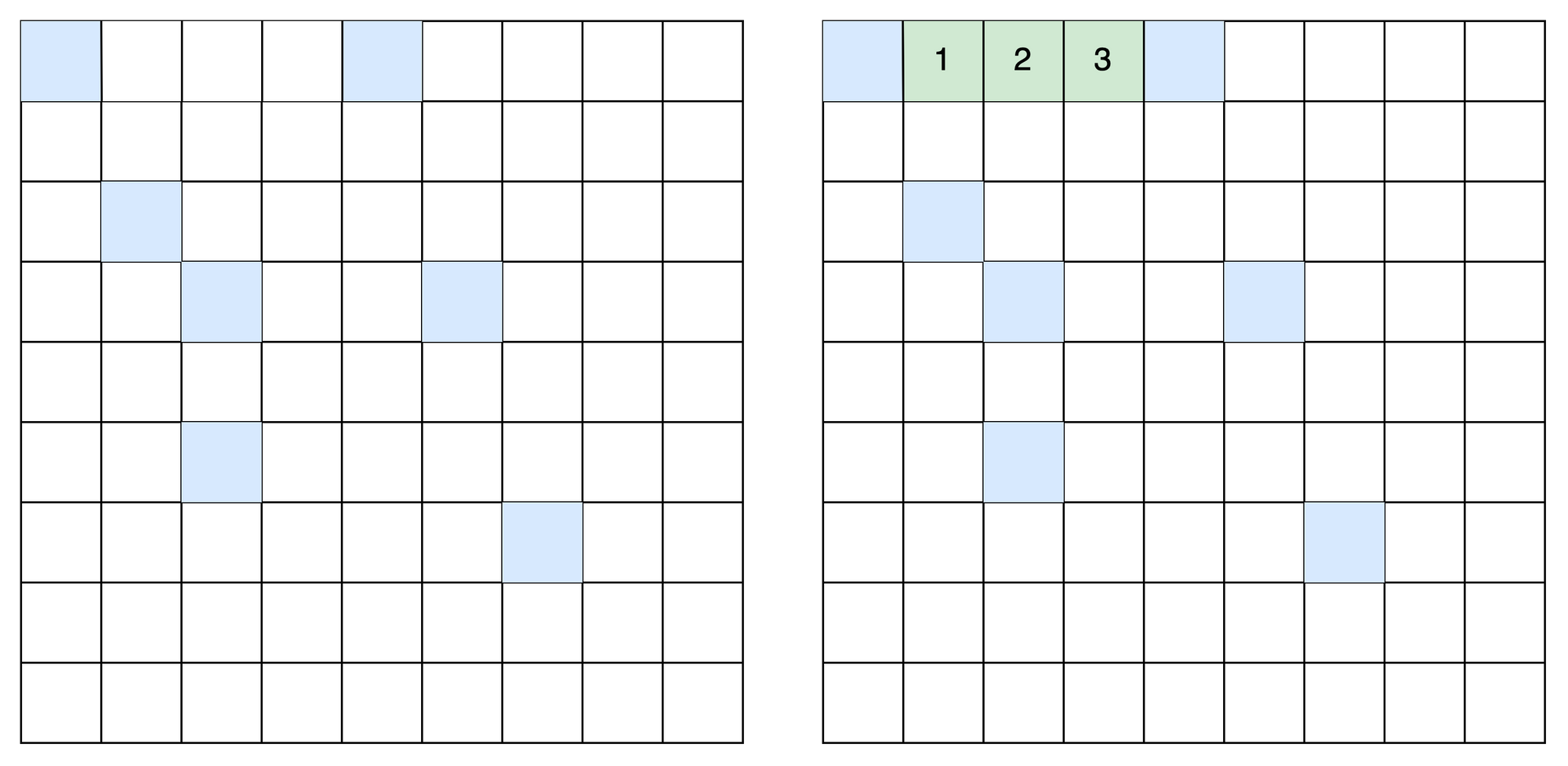
When an array is declared, the program allocates a contiguous (adjacent) set of empty cells in memory. So by creating a three element array, the machine will find a group of empty cells and designate it to store the array:
x = [1, 2, 3]
Lookups / Reads
Every cell in the computer's memory has an "address" which are sequential: 1000, 1001, 1002. Whenever memory is allocated for an array, the computer also records the "address".
When looking up an array's value at any given index, the machine knows the array's "address" and can quickly find a value by locating the array in memory and jumping to the correct index in one step or constant time: O(1) regardless of the length of the array.
Updates / Modifications
Updates are also very efficient because the computer knows the address of the array in memory and can quickly jump to the index and replace the value.
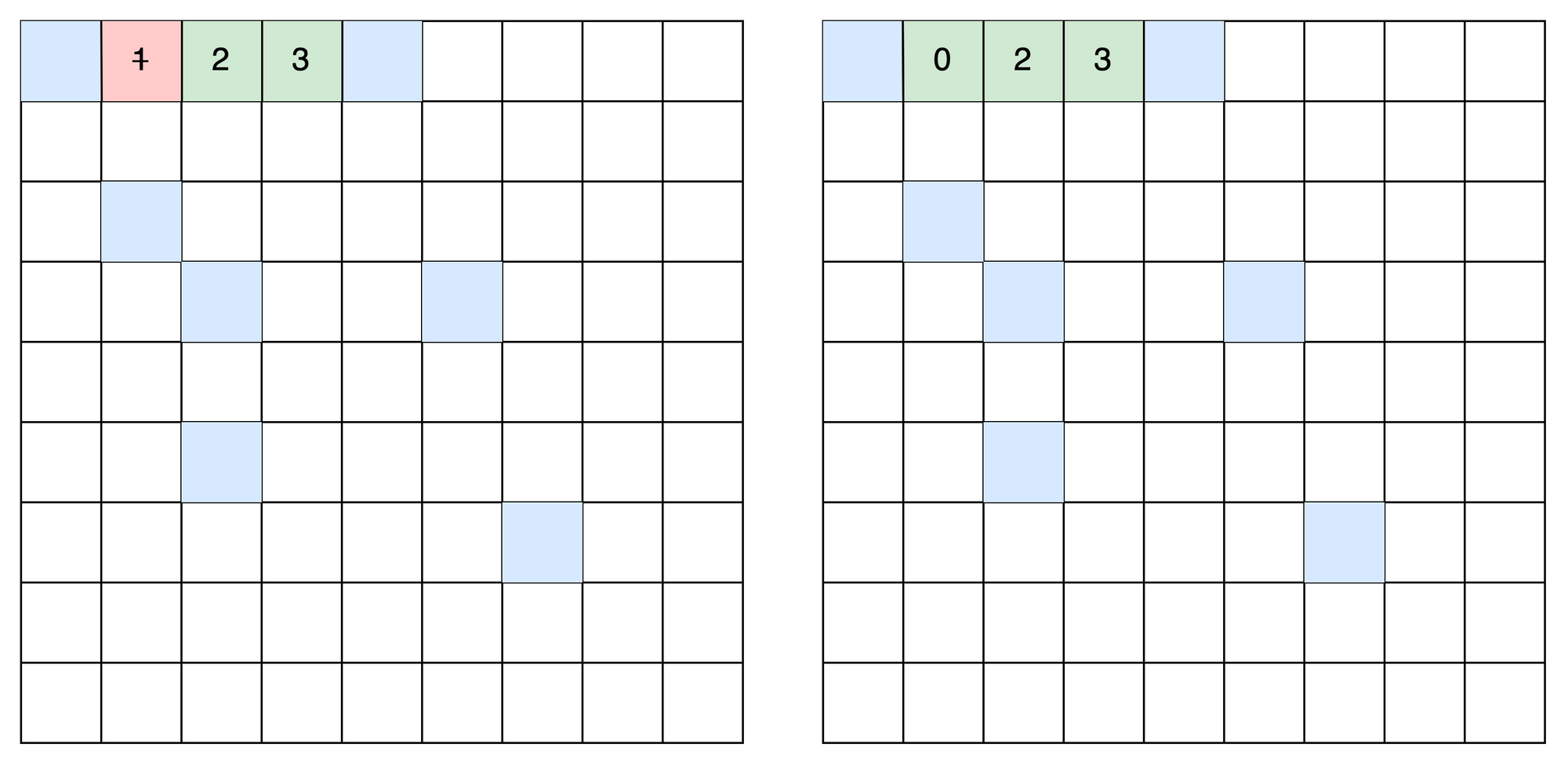
But to demonstrate the ephemeral nature of an imperative array, let's look at an example in Ruby. We first assign the array to x and re-assign at index 0.
x = [1, 2, 3]
print "before: #{x}\n"
x[0] = 0
print "after: #{x}\n"Running this program will print:
before: [1, 2, 3]
after: [0, 2, 3]Assigning a new value at index 0 was a destructive operation and the array's value becomes: x = [0, 2, 3]
The values are ephemeral and it's not difficult to imagine a scenario where concurrent, competing operations must share access to a single resource which is normally where thread locking mechanisms are introduced:
semaphore = Mutex.new
a = Thread.new {
semaphore.synchronize {
# access shared resource
}
}
b = Thread.new {
semaphore.synchronize {
# access shared resource
}
}Ephemeral Values
Lookup and Update operations are extremely efficient in imperative settings because again, the machine can access values in a single step. This efficiency however is made possible by destructive assignment as a program performs state transitions. This characteristic can also be a double-edged sword in terms of dealing with concurrency and the correctness of a program in any context.
Lists vs Arrays in Elixir and Erlang
Briefly, lists are implemented as singly-linked lists in Elixir and Erlang. They're comprised of a collection of nodes that can be stored non-contiguously because each node has a link to the next node's "address" in memory. Here's an example of [1, 2, 3]:
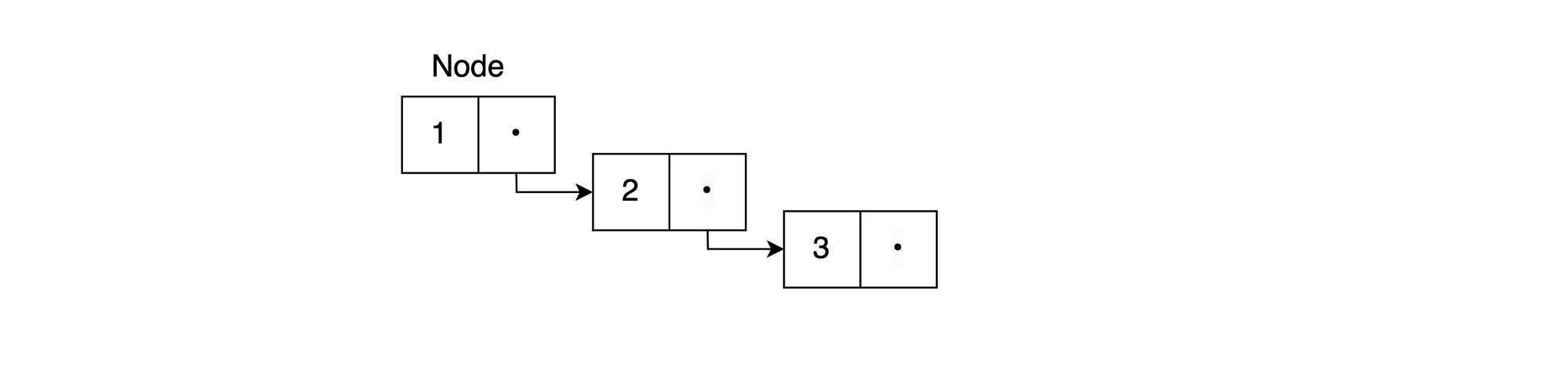
Adding new nodes to the head of the list is an efficient, constant time operation O(1) because the VM only has to create one new cell in memory which is then linked to the tail. This operation is referred to as cons or "Construct a List".
(Reading and updating a list's head value are also constant-time operations for the same reasons).
All other operations (including calculating the list's length) require traversing the list starting at the head in order to find the memory address of each subsequent node O(n).
Tuples vs Arrays
Again, we'll briefly touch on how tuples in Elixir and Erlang compare to imperative arrays because we're building up to how functional arrays are implemented in Erlang.
Tuples are implemented more closely to imperative arrays in that they're stored contiguously in memory. Here's an example of {1, 2, 3}

The Tuple's length or arity is stored as the first element in memory enabling constant time O(1) length lookups.
Random access lookup operations (get value at index) can also be performed in constant time O(1) just like imperative arrays because the VM knows the Tuple's address in memory which is sequential, and can quickly jump to any element by simple addition.
But because we're in a functional setting with persistent values, update operations need to traverse the entire Tuple, copy each element with the modified one to a new location in memory leaving the original intact O(n).
Nested Tuples
Finally, Tuples can be nested and each nested Tuple can be stored in different locations in memory connected by pointers or references. Here's an example using: {:ok, {:status, 418, "I'm a teapot"}}

Updating a child tuple doesn't require copying the entire parent, only the pointer to the new child's address in memory.
:array implementation from the Erlang standard library. Functional Array Implementation
With the preceding details in mind, let's explore the functional array implementation available in the Erlang standard library using Elixir.
First, using :array.new/0 returns a tuple:
iex> :array.new()
{:array, 0, 10, :undefined, 10}This stores a cache for the array size, max size, default value and the elements of the array.
fixed size so the array doesn't expand beyond max limit, but we'll gloss over these details for now.Next, let's build an array from a list using [1, 2, 3] :
iex> :array.from_list([1, 2, 3])
{:array, 3, 10, :undefined,
{1, 2, 3, :undefined, :undefined, :undefined, :undefined, :undefined, :undefined, :undefined}}At first glance, this representation might seem confusing, but remember the values at each position: {:array, size, max, default, elements}.
The size of the array is 3, the max has defaulted to 10, the default value for an unassigned element is :undefined (also configurable) and finally, the elements of the array are:
{1, 2, 3, :undefined, :undefined, :undefined, :undefined, :undefined, :undefined, :undefined}But why are there 10 elements when we've only declared 3?
Tree Structure
Arrays are implemented with a variation of an M-Ary Tree Data Structure and have a leaf size or fanout of 10.
A leaf is a node of the tree that doesn't have any children. Currently our Array's tree structure consists of a single leaf with 10 elements, three of which have values assigned:

Here are some more details outlined in the source code:
A tree is either:
- a leaf, with LEAFSIZE elements (the "base")
- an internal node with LEAFSIZE+1 elements
- an unexpanded tree, represented by a single integer: the number of elements that may be stored in the tree when it is expanded.
Each leaf has a base size of 10 meaning that the leaf is filled out to 10 elements even if there aren't 10 values to store. The reason for this will become more clear as we continue through the implementation.
Expanding the Tree
When 0-10 values are assigned, the tree structure will always have a single leaf:
iex> list = ["v1", "v2", "v3", "v4", "v5", "v6", "v7", "v8", "v9", "v10"]
iex> :array.from_list(list)
{:array, 10, 10, :undefined,
{"v1", "v2", "v3", "v4", "v5", "v6", "v7", "v8", "v9", "v10"}}The elements are a 10-element tuple containing the values we assigned.
Let's see what happens when we build an array with 11 elements:
iex> list = ["v1", "v2", "v3", "v4", "v5", "v6", "v7", "v8", "v9", "v10", "v11"]
iex> :array.from_list(list)
{:array, 11, 100, :undefined,
{{"v1", "v2", "v3", "v4", "v5", "v6", "v7", "v8", "v9", "v10"},
{"v11", :undefined, :undefined, :undefined, :undefined, :undefined,
:undefined, :undefined, :undefined, :undefined}, 10, 10, 10, 10, 10, 10, 10,
10, 10}}The representation has changed, but we can still see that values are grouped and padded into 10-element tuples.
Zooming in on just the elements:
{
{"v1", "v2", "v3", "v4", "v5", "v6", "v7", "v8", "v9", "v10"},
{"v11", :undefined, :undefined, :undefined, :undefined, :undefined, :undefined, :undefined, :undefined, :undefined},
10, 10, 10, 10, 10, 10, 10, 10, 10
}The first element of the parent tuple makes sense, it holds the first ten values. The second element is another ten element tuple with only the first value assigned and the rest are :default values.
But what are the other values of 10?
Remember the different types of trees:
- a leaf, with LEAFSIZE elements (the "base")
- an internal node with LEAFSIZE+1 elements
- an unexpanded tree, represented by a single integer
We can now see all three tree variations being used:
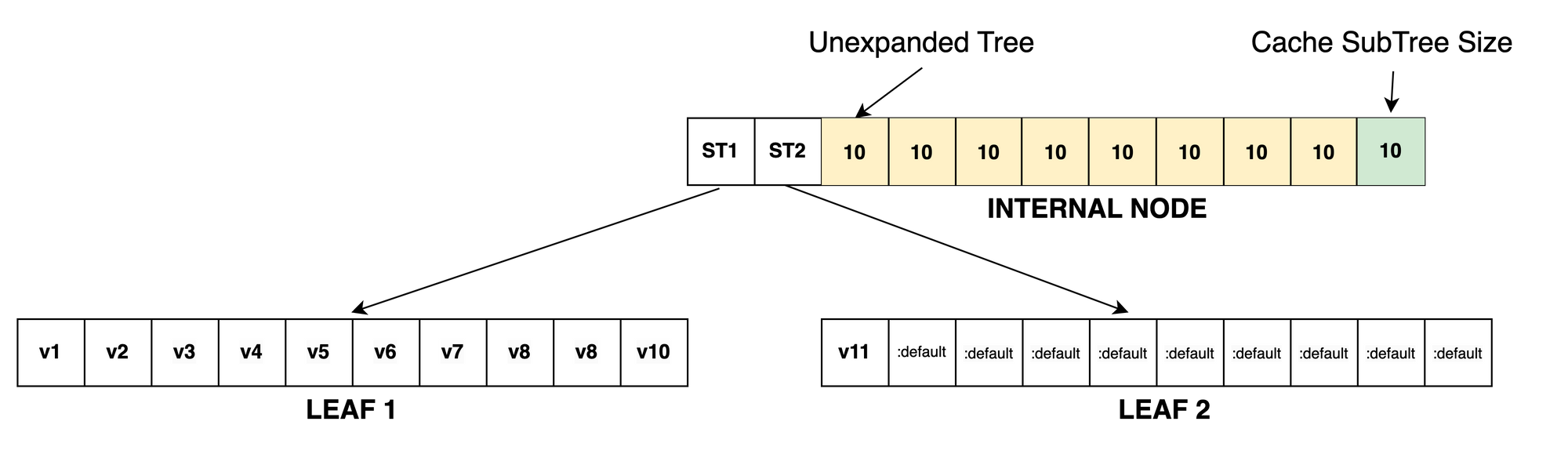
Internal nodes have leafsize + 1 elements, the last being a cache for how many elements are stored in the sub-trees. This detail comes into play when performing lookup or update operations which we'll look at next.
Functional Array Operations
You may be wondering why go through all of this to implement an array?
The reason is memory efficiency and performance. In scenarios where you need both efficient random access and efficient updates, neither a list nor a tuple can support both.
When using lists, accessing and prepending elements on the head is efficient O(1), but random access (lookups) for an element at a given index requires traversing the list and in the worst-case the entire list which is O(n).
When using tuples, random access is efficient O(1), but modifying an element requires traversing the entire tuple and copying the elements, also O(n).
Let's look at how lookups and updates work with Erlang's functional array implementation.
Functional Array - Random Access
Sticking with our 11-element array example, we'll be using a slimmed-down Elixir implementation of an Array tree structure to help illustrate the ideas.
Array module to help unpack the implementation. Again, we're doing just enough to get the ideas across so this isn't a 1-to-1 implementation.Given our previous example:

We have a simple, Elixir flavoured Array struct that sets some defaults and defines the struct:
defmodule Array do
@moduledoc """
An Elixir Array implementation for simple get/set operations.
"""
@default :undefined
@leafsize 10
@nodesize @leafsize
defstruct [:size, :max, :elements, default: @default]
endFirst, build the list using the Elixir version:
iex> array = Array.from_list(list)
%Array{
size: 11,
max: 100,
elements: {{"v1", "v2", "v3", "v4", "v5", "v6", "v7", "v8", "v9", "v10"},
{"v11", :undefined, :undefined, :undefined, :undefined, :undefined,
:undefined, :undefined, :undefined, :undefined}, 10, 10, 10, 10, 10, 10, 10,
10, 10},
default: :undefined
}This should all look familiar apart from being wrapped in an Array struct.
Next, let's get the value at index 5:
iex> Array.get(5, array)
"v6"First Iteration
Stepping through the Elixir version of the code to find this value:
def get(index, array) when is_integer(index) and index >= 0 do
cond do
index < array.size -> get_1(index, array.elements, array.default)
array.max > 0 -> array.default
true -> :erlang.error(:badarg)
end
endThis root function checks for valid arguments and will either continue searching or return the :default value.
We passed a valid index, so stepping into get_1/3 we first pattern match on the value of elements to determine if we're currently on an Internal Node (Does the leaf have an extra element?).
defp get_1(index, {_, _, _, _, _, _, _, _, _, _, s} = elements, default) do
rem_index = rem(index, s)
elem_index = div(index, s) + 1
element = :erlang.element(elem_index, elements)
get_1(rem_index, element, default)
end
defp get_1(_index, elements, default) when is_integer(elements), do: default
defp get_1(index, elements, _D), do: :erlang.element(index + 1, elements)
In our example, we have an internal node wrapping the leaves or sub-trees. This is where the cached sub-tree size comes into play:

First we calculate the remainder of dividing the given index by sub-tree size:
# index = 5, s = 10
rem_index = rem(index, s) = 5Then, the element index by dividing the given index by sub-tree size:
# index = 5, s = 10
elem_index = div(index, s) + 1 = 1This helps to select the right sub-tree that contains the element at the given index.
Next, we select the element from the nested tuple at the element index:
# elem_index = 1
element = :erlang.element(elem_index, elements)
This selects the sub-tree at position 1 from the current node, and recursively passes the new values to itself:
get_1(rem_index, element, default)
Second Iteration
At this point we've checked the Internal Node and selected the correct internal sub-tree which contains the value at the given index:
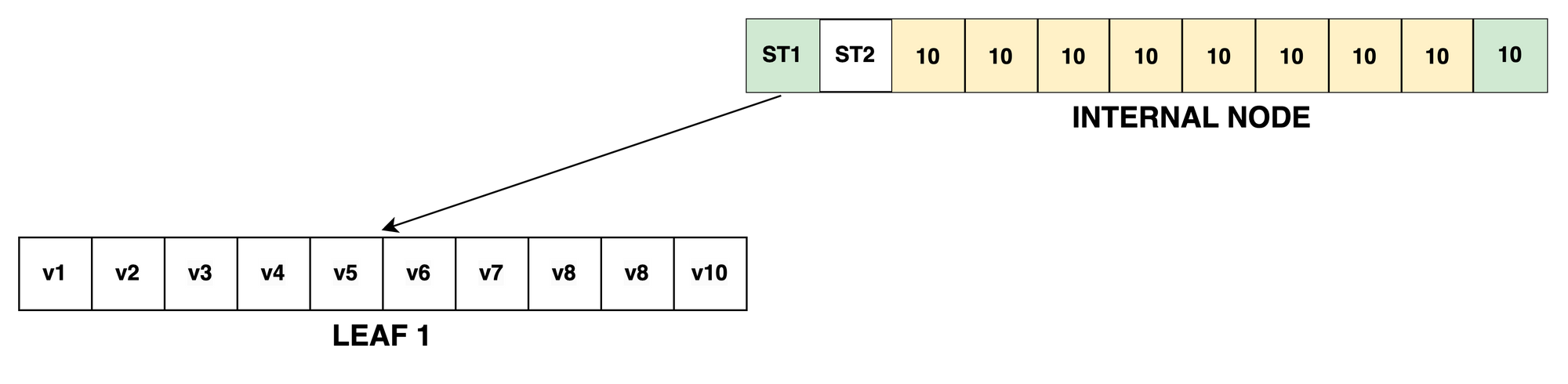
The recursive get_1/3 function again:
defp get_1(index, {_, _, _, _, _, _, _, _, _, _, s} = elements, default) do
...
end
defp get_1(_index, elements, default) when is_integer(elements), do: default
defp get_1(index, elements, _default), do: :erlang.element(index + 1, elements)This time around, elements contains the leaf values as a tuple without the extra element:
index = 5
elements = {"v1", "v2", "v3", "v4", "v5", "v6", "v7", "v8", "v9", "v10"}So it's handled by the last function head:
defp get_1(index, elements, _default), do: :erlang.element(index + 1, elements)This selects the element at index + 1 (tuples have 1-based indices) which in our example happens to be v6.
Time Complexity
To break down a lookup operation on this tree implementation where n is the length of the array and n = 11
First Iteration - Internal Node:
- calculate indices:
2 steps - select element:
1 step - total:
3 steps
Second Iteration - Leaf:
- select element:
1 step
Total: 4 Steps
Here's an overview of how the number of steps changes as the array length increases:
| n | steps |
|---|---|
| 0-10 | 1 |
| 11-100 | 4 |
| 101-1,000 | 7 |
| 1,001-10,000 | 10 |
For every factor of ten, only three more steps are needed to perform random access operations. This is logarithmic, base-10 time complexity or O(log10 n) and after dropping constants: O(log n).
This is major performance improvement over O(n) worst-case scenarios with Lists.
Functional Array - Updates
In our scenario we need both efficient random access lookups and efficient updates or modifications. We've established that this tree data structure enables efficient lookups, but how do modifications work?
Traversing the tree structure works exactly the same way as lookups, except this time when the correct leaf is found, the element at the given index is modified.
For example, let's update the value at index 5 from the previous example where we've recursed the tree and found the correct leaf:
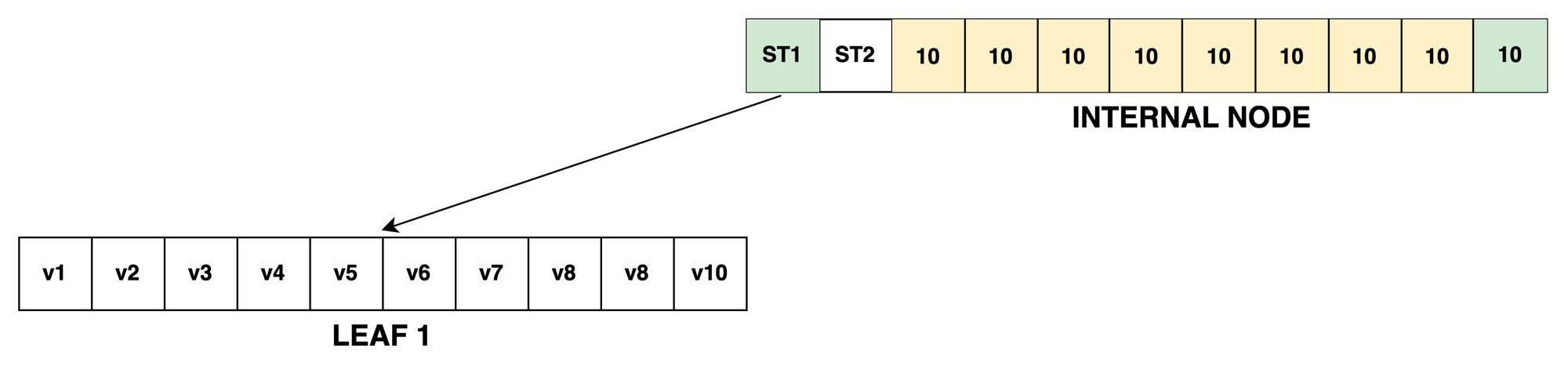
The leaf tuple is then traversed and copied with a NEW value at index 5:
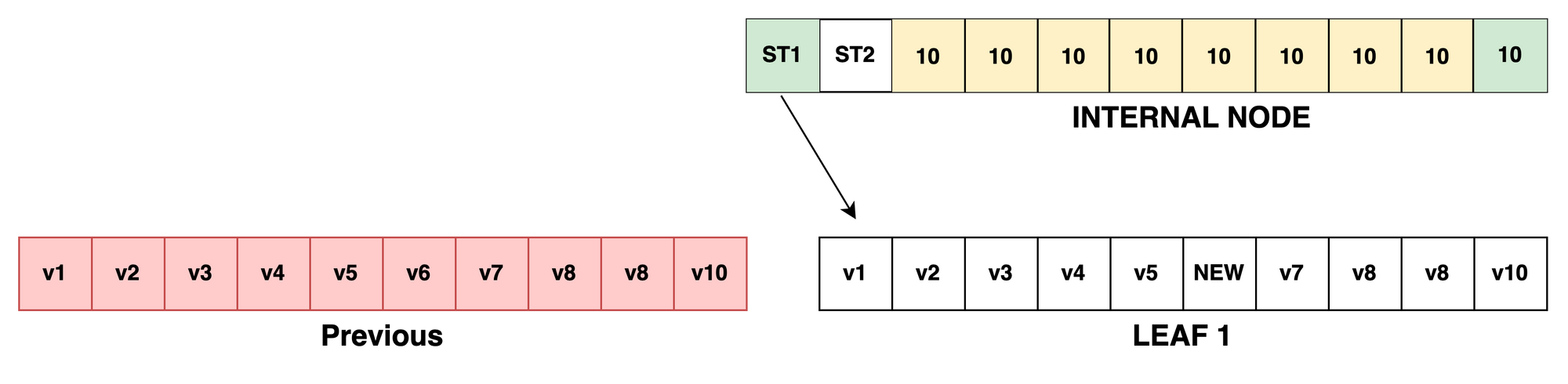
As discussed previously, parent elements in Tuples hold references to their children so only the 10-element tuple that contains the given index is copied and the parent's reference or pointer to the new child tuple is updated.
These details give the :array tree data structure a good balance between read (random access) and update performance by minimizing operations and allocating new tuples only when necessary.
Updating an entry gives you a reference to a conceptually "new" array but most of the data is reused and shared with the previous version.
Time Complexity
O(log n)
Wrapping up
This has been a trek stepping through various concepts, comparing imperative arrays to functional implementations but thanks for sticking with me.
Erlang arrays were implemented because the creators of Wings3D (http://www.wings3d.com/) needed a more performant data structure than :gb_trees, which are likely binary trees that have O(log2 n). I haven't looked into it but this implementation would theorectically need 5x more steps to perform the same get/set operations.
The main thrust here is that by understanding some of the fundamental differences between functional programming settings versus imperative settings, we can make informed decisions about which data structures will perform best for a particular use case. In situations when none are readily available, it's possible to create custom data structures using standard building blocks and still maintain the benefits of immutability or persistence for concurrent operations.
Book
I'm in the process of writing a book for Elixir/Erlang developers dive deeper into functional data structures.
Subscribe to the free newsletter for updates and progress!
-- Troy
Twitter: @tmartin8080 | ElixirForum