LeetCode - Median of Two Sorted Arrays | Elixir Solution

Finding the median of two sorted arrays can be accomplished in a straight-forward way with an O(n) solution.  

Admittedly,  improving the performance of this problem's brute force approach proved to be rather difficult, and I hope that as we walk through the Binary Search approach together, the benefits become apparent.

Problem

Given two sorted arrays nums1 and nums2 of size m and n respectively, return the median of the two sorted arrays.

The overall run time complexity should be O(log(m+n)).

Example 1:

Input: nums1 = [1,3], nums2 = [2] 
Output: 2.00000 
Explanation: merged array = [1,2,3] and median is 2.

Example 2:

Input: nums1 = [1,2], nums2 = [3,4] 
Output: 2.50000 
Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.

Constraints:

• nums1.length == m
• nums2.length == n
• 0 <= m <= 1000
• 0 <= n <= 1000
• 1 <= m + n <= 2000
• -106 <= nums1[i], nums2[i] <= 106

Solution - Binary Search

defmodule Solution do
  # constraints
  @neginf :math.pow(10, 6) * -1
  @posinf :math.pow(10, 6)

  @spec find_median_sorted_arrays(nums1 :: [integer], nums2 :: [integer]) :: float
  def find_median_sorted_arrays(nums1, nums2) do
    {{a1, m}, {a2, n}} = shortest_first(nums1, nums2)
    range = {0, max(m, 0)}
    find_median(range, {a1, m}, {a2, n})
  end

  defp find_median({low, high}, {a1, m}, {a2, n}) do
    {a1_partition, a2_partition} = partition_arrays({low, high}, m, n)

    a1_max_left = if a1_partition == 0, do: @neginf, else: :array.get(a1_partition - 1, a1)
    a1_min_right = if a1_partition == m, do: @posinf, else: :array.get(a1_partition, a1)
    a2_max_left = if a2_partition == 0, do: @neginf, else: :array.get(a2_partition - 1, a2)
    a2_min_right = if a2_partition == n, do: @posinf, else: :array.get(a2_partition, a2)

    cond do
      # found correct partition
      a1_max_left <= a2_min_right and a2_max_left <= a1_min_right ->
        max_left = max(a1_max_left, a2_max_left)
        min_right = min(a1_min_right, a2_min_right)

        if Integer.mod(m + n, 2) == 0 do
          (max_left + min_right) / 2
        else
          max_left
        end

      # incorrect partition, shift left
      a1_max_left > a2_min_right ->
        new_high = a1_partition - 1
        find_median({low, new_high}, {a1, m}, {a2, n})

      # incorrect partition, shift right
      true ->
        new_low = a1_partition + 1
        find_median({new_low, high}, {a1, m}, {a2, n})
    end
  end

  # convert to actual arrays and sort by ascending length
  defp shortest_first(nums1, nums2) do
    a1 = :array.from_list(nums1)
    a2 = :array.from_list(nums2)
    a1_length = :array.size(a1)
    a2_length = :array.size(a2)

    if a1_length <= a2_length do
      {{a1, a1_length}, {a2, a2_length}}
    else
      {{a2, a2_length}, {a1, a1_length}}
    end
  end

  defp partition_arrays({low, high}, m, n) do
    a1_partition = round((low + high) / 2)
    a2_partition = round((m + n) / 2 - a1_partition)
    {max(a1_partition, 0), max(a2_partition, 0)}
  end
end

TLDR;

1. Start with the shortest array
2. Partition arrays on left | right so all values on left are < all values on the right.
   - If there are no values to compare, use @neginf on left, and @posinf on right.
   - Shift partitioning left, right until true.
3. Median - Odd vs Even
   - When the size of combined arrays is even, take the max of left values.
   - When the size of combined arrays is odd, take the average of max_left + max_right values.

Time Complexity: O(log(m+n))

Source: https://github.com/tmartin8080/leet

Approach and Explanation

Let's walk through each step of the approach starting with defining some terms within the problem.

What is a Median?

Here's a definition of median:

a value or quantity lying at the midpoint of a frequency distribution of observed values or quantities, such that there is an equal probability of falling above or below it

When the array has an odd number of elements, we take the middle value and in this case the median is 3:

When array length is even, we take the average of the two middle elements.  Here the median is (3 + 3) / 2 = 3.

Approach 1: Brute Force - Merge Arrays

With a brute force approach, we can merge the values of both arrays and find the median of the new, merged array:

The new merged array is odd so the median is the center value:

Complexity Analysis

To merge both arrays, we'll need to step through each element for each array which will result in a time complexity of O(m+n) and after dropping constants: O(n).

This results in linear time complexity and though it solves most of the problem, it's not efficient enough.

Approach 2: Binary Search

The problem requires an algorithm with O(log(m+n)) so let's see how we can improve efficiency by using Binary Search.

Binary Search - Algorithm Overview

Briefly, binary search has logarithmic complexity because when the length of inputs is doubled, only one extra step is required.

As an example, think of finding a business in an old phone book.  You'd start by opening the book somewhere in the middle and if the current character index is too low, split the latter half and check again.

There are three key steps involved in the binary search solution:

Step 1

Start with the shortest array as a1:

Step 2

Partition both arrays so that every element in the left partition is less than every element in the right partition (more on this soon).

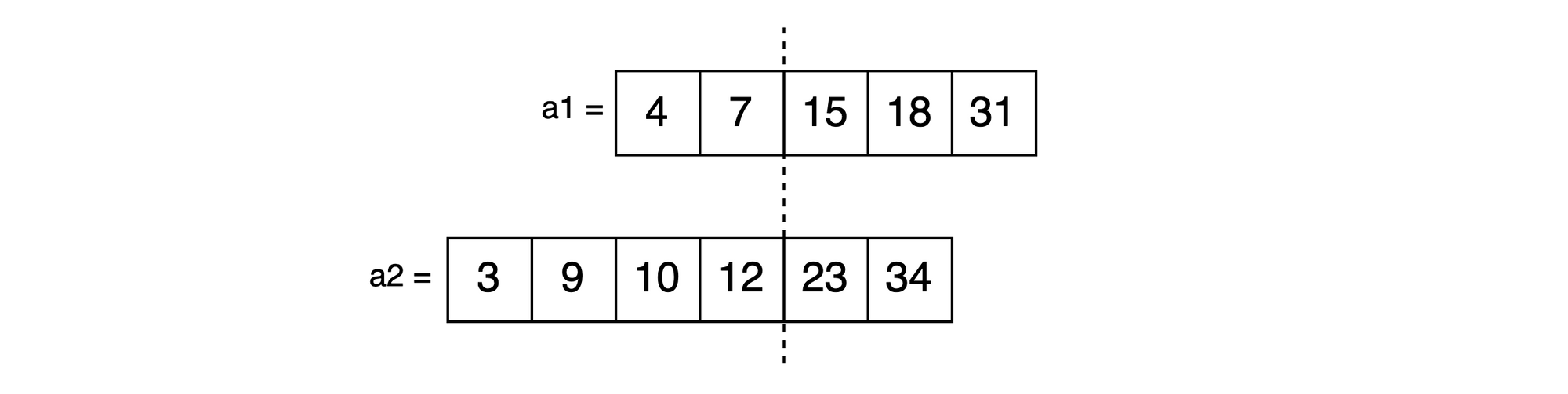
Step 3

When values on each side of the partition meet both following conditions, we've found the correct partition:

Condition 1: left max a1 (7) <= right min a2 (23):

Condition 2: left max a2 (12) <= right min a1 (15):

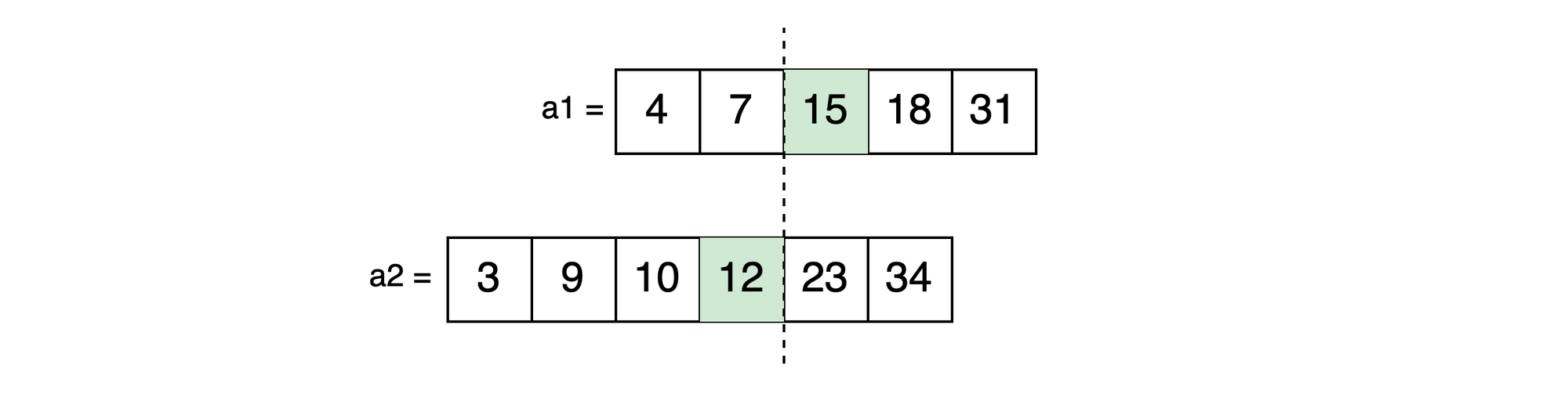
When both conditions are met, we've found our partition and calculate the median.

Partitioning is the crux of this algorithm so don't worry if it doesn't quite make sense yet. We'll walk through this example in greater detail soon.

Calculating Median

After finding the correct partition, we calculate the median differently when the length of both arrays combined is odd vs even. (Our example is odd: 11)

Odd Total: highest of the left max values of both arrays:

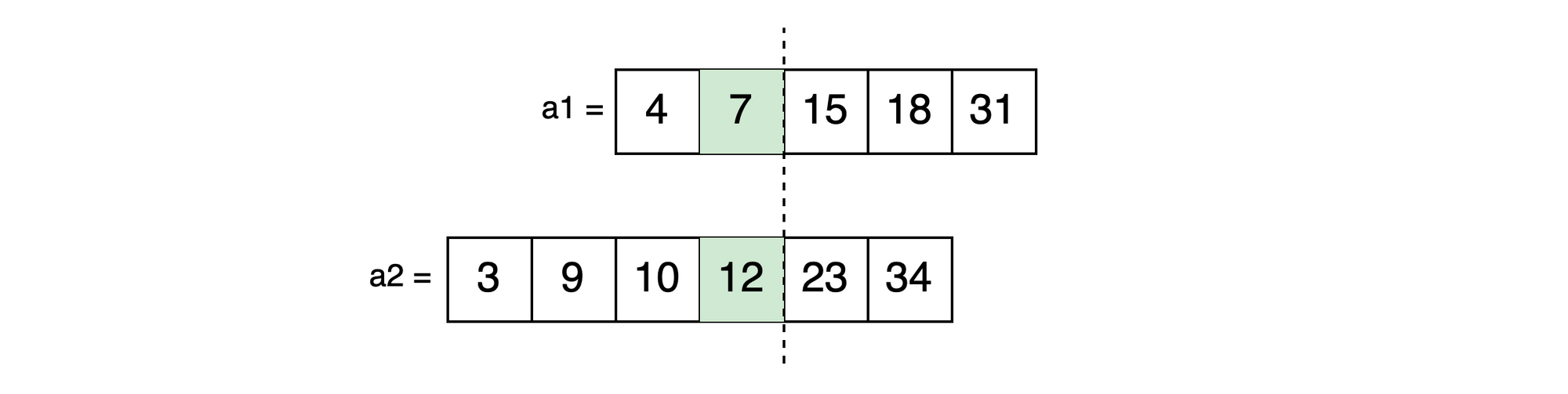
max(left-a1, left-a2) OR max(7, 12) = 12

Even Total: We don't have an example here yet, but you would take the average of the highest left value of both arrays and the lowest right value from both arrays: avg(max(left-a1, left-a2), min(right-a1, right-a2)) .

This is the core of the solution so if this doesn't make sense yet, maybe skim through the details again before continuing to the implementation.

Algorithm Implementation

We'll use the same example as above where the median is 12:

Step 1 - Start with Shortest Array

Starting with the prompt, we'll find the shortest array and assign it to a1:

def find_median_sorted_arrays(nums1, nums2) do
  {{a1, m}, {a2, n}} = shortest_first(nums1, nums2)
end

# convert to :arrays and place shortest first
# O(N) but this is a flaw with the problems input
# ignore this glaring detail for now :)
defp shortest_first(nums1, nums2) do
  a1 = :array.from_list(nums1)
  a2 = :array.from_list(nums2)
  a1_length = :array.size(a1)
  a2_length = :array.size(a2)

  if a1_length <= a2_length do
    {{a1, a1_length}, {a2, a2_length}}
  else
    {{a2, a2_length}, {a1, a1_length}}
  end
end

The prompt passes Lists as arguments so we are converting to arrays (which is an O(N) operation) but let's ignore this worse-case scenario for the time being and imagine the inputs are already :arrays :)

Benchmarks  - :array vs List

Here are some rough benchmarks for List vs :array:

## Count
Comparison:
:array.size/1       11.66 M
Enum.count/1       0.0632 M - 184.57x slower +15.75 μs

## Get
Comparison:
:array.get/2        6.75 M
Enum.at/2         0.0839 M - 80.41x slower +11.77 μs

With that out of the way, let's get back to our problem.

Step 2 - Partition Arrays

At this point we're certain that a1 is the shortest array.  

Next, let's establish how we kick-off Binary Search by partitioning the arrays.

Starting with the shortest array, we determine how many ways it can be partitioned to create lower and upper bounds:

def find_median_sorted_arrays(nums1, nums2) do
  {{a1, m}, {a2, n}} = shortest_first(nums1, nums2)
  range = {0, max(m, 0)}
  find_median(range, {a1, m}, {a2, n})
end

Then pass the input data and initial range to our main recursive function:

defp find_median({low, high}, {a1, m}, {a2, n}) do
  {a1_partition, a2_partition} = partition_arrays({low, high}, m, n)
end

defp partition_arrays({low, high}, m, n) do
  a1_partition = round((low + high) / 2)
  a2_partition = round((m + n) / 2 - a1_partition)
  {max(a1_partition, 0), max(a2_partition, 0)}
end

Remember, we don't know where to partition yet so we start off the Binary Search by partitioning A1 somewhere in middle:

# low = 0, high = 5
a1_partition = round((low + high) / 2)

And partition A2so there are approximately an even number of elements on left/right based on A1's partition:

# m = 5, n = 6, a1_partition = 3
a2_partition = round((m + n) / 2 - a1_partition)

Here's where our first partition pass split left | right values:

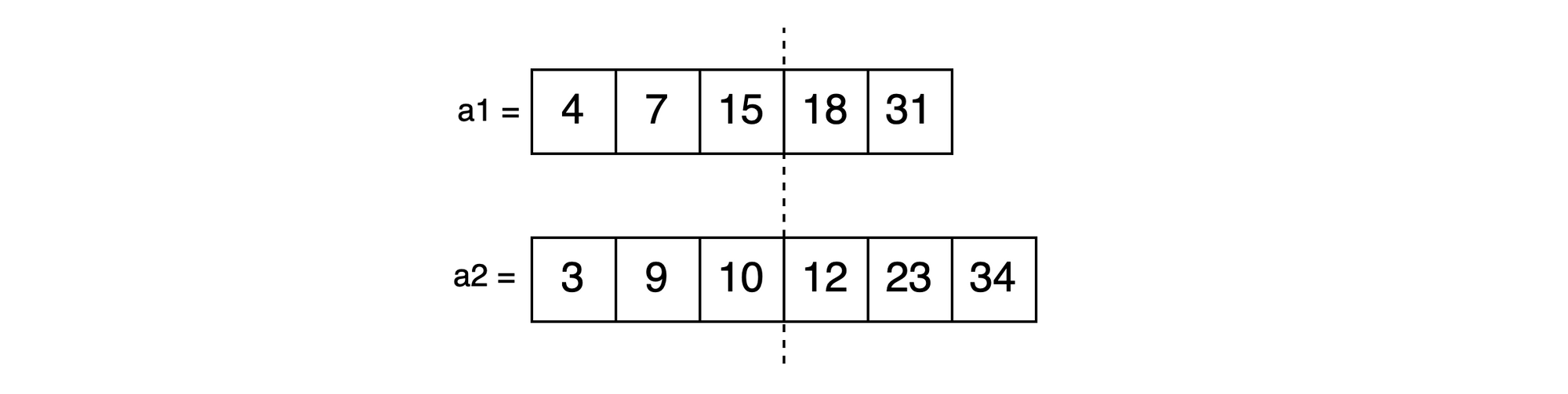
To account for this, we've defined the constraints as:

@neginf :math.pow(10, 6) * -1
@posinf :math.pow(10, 6)

Check Conditions - Step 3

Next, we assign values on either side of the partition and use our constraints as defaults when we reach the edges of each array's boundaries:

a1_max_left = if a1_partition == 0, do: @neginf, else: :array.get(a1_partition - 1, a1)
a1_min_right = if a1_partition == m, do: @posinf, else: :array.get(a1_partition, a1)
a2_max_left = if a2_partition == 0, do: @neginf, else: :array.get(a2_partition - 1, a2)
a2_min_right = if a2_partition == n, do: @posinf, else: :array.get(a2_partition, a2)

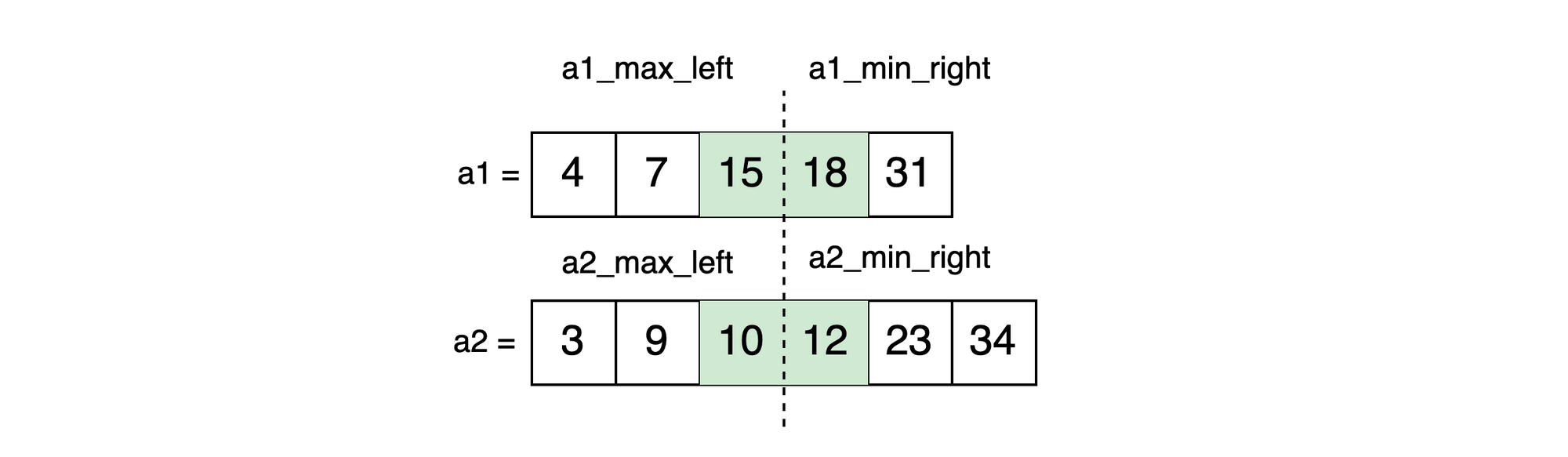
A1's partition is 3, so we use a1_partition - 1 in order to select the value left of the partition:

To check if we've found the right partition we use a cond statement:

cond do
  a1_max_left <= a2_min_right and a2_max_left <= a1_min_right ->
    # correct partition, calculate median

  a1_max_left > a2_min_right ->
    # incorrect partition, shift LEFT

  true ->
    # incorrect partition, shift RIGHT
end

Stepping through the conditions we can see that we have NOT found the correct partition on the first guess:
1. 15 <= 12 = false -> false, continue to next condition
2. 15 > 12 = true -> true, shift partitions LEFT

Shift Partitions Left

Let's fill out the rest of this condition statement and continue:

cond do
  ...

  # shift upper bound left
  a1_max_left > a2_min_right ->
    new_high = a1_partition - 1
    find_median({low, new_high}, {a1, m}, {a2, n})

  ...
end

We shift A1's partitioning upper bound one to the left.  A2's partition is based on A1's, that's all we have to do, so simply re-call the recursive function to shift the partition and re-check the conditions.

Second Iteration

On the second iteration we'll shift partitioning to the left.  Here's the partitioning function again:

# low = 0, high = 2
defp partition_arrays({low, high}, m, n) do
  a1_partition = round((low + high) / 2)
  a2_partition = round((m + n) / 2 - a1_partition)
  {max(a1_partition, 0), max(a2_partition, 0)}
end

Based on these formulas a1_partition becomes 1 and a2_partition becomes 5 and we partition the arrays at the new positions:

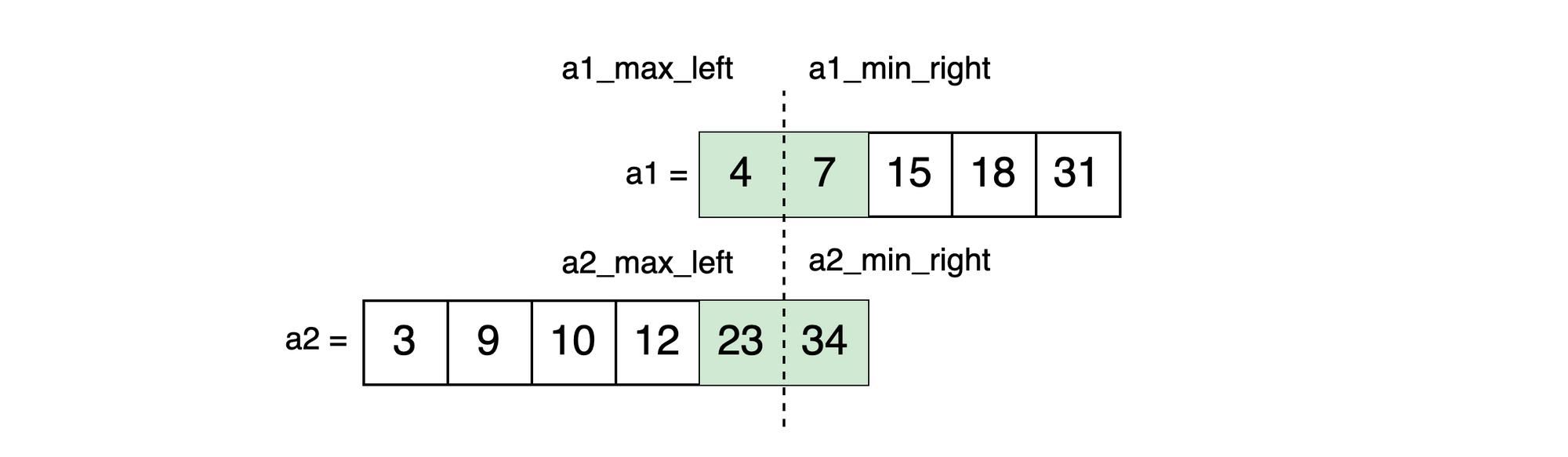
Again, checking the conditions for truthiness:

cond do
  a1_max_left <= a2_min_right and a2_max_left <= a1_min_right ->
    # correct partition, calculate median

  a1_max_left > a2_min_right ->
    # incorrect partition, shift LEFT

  true ->
    # incorrect partition, shift RIGHT
end

1. 4 <= 34 = true and 23 <= 7 = false -> false, check next condition
2. 4 > 34 = false -> false, check next condition
3. true -> true, shift right

Shift Partitions Right

We've shifted the partitions but now we're in the opposite position.  A value on the left is greater than a value on the right.

 

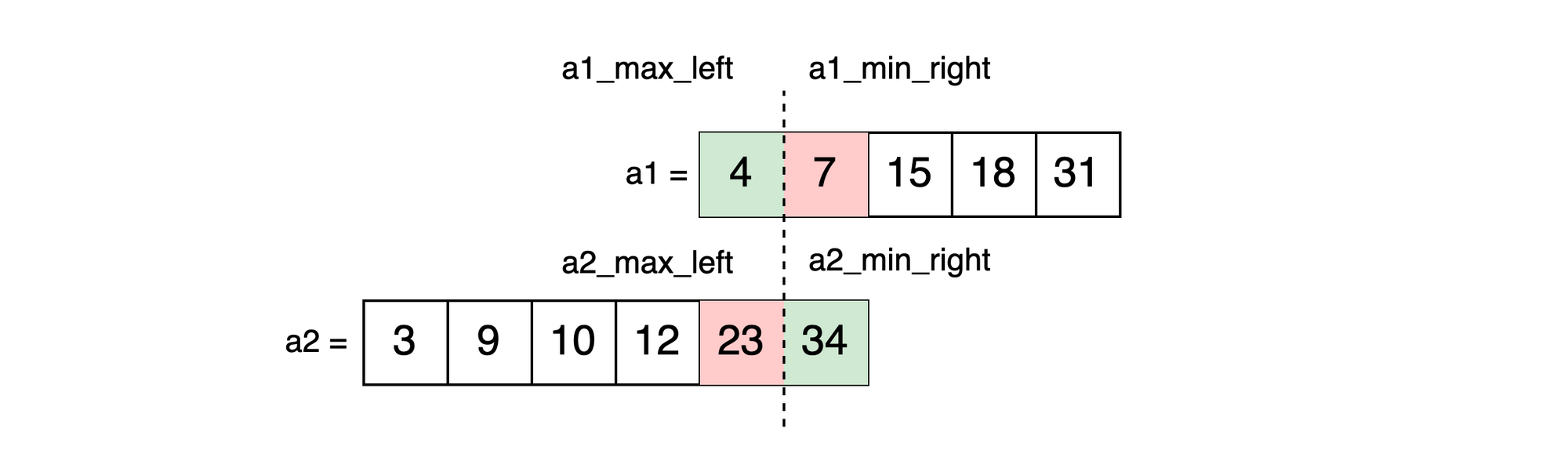
To correct, we shift the partitioning to the right by increasing the lower bound for A1's partition:

# a1_partition = 1 (at this point)
cond do
  ...

  # shift lower bound right
  true ->
    new_low = a1_partition + 1
    find_median({new_low, high}, {a1, m}, {a2, n})
end

Again, we're only adjusting the range for A1 because A2's partition is based on A1's.

Third Iteration

Let's try again and update the partitions:

# low = 2, high = 2
defp partition_arrays({low, high}, m, n) do
  a1_partition = round((low + high) / 2)
  a2_partition = round((m + n) / 2 - a1_partition)
  {max(a1_partition, 0), max(a2_partition, 0)}
end

Which results in:

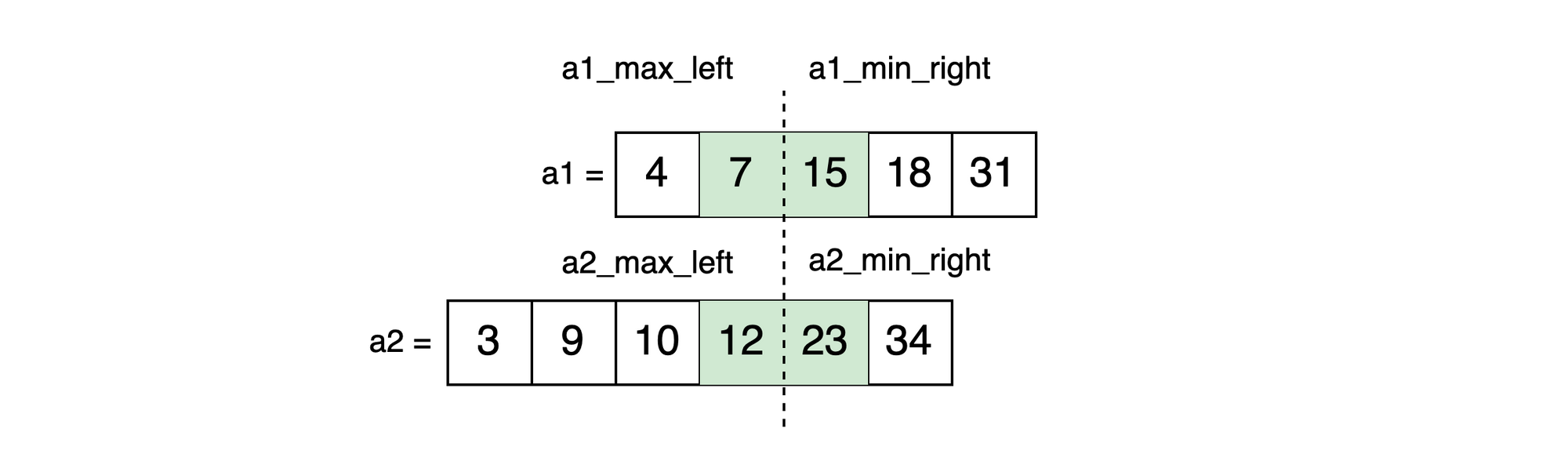
And when we check the conditions:

cond do
  a1_max_left <= a2_min_right and a2_max_left <= a1_min_right ->
    # correct partition, calculate median

  a1_max_left > a2_min_right ->
    # incorrect partition, shift LEFT

  true ->
    # incorrect partition, shift RIGHT
end

1. 7 <= 23 = true and 12 <= 15 = true -> true, calculate median.

Finally, we have found the correct partition and it only took 3 recursive iterations.

Calculating Median

Here is our current partition and the values:

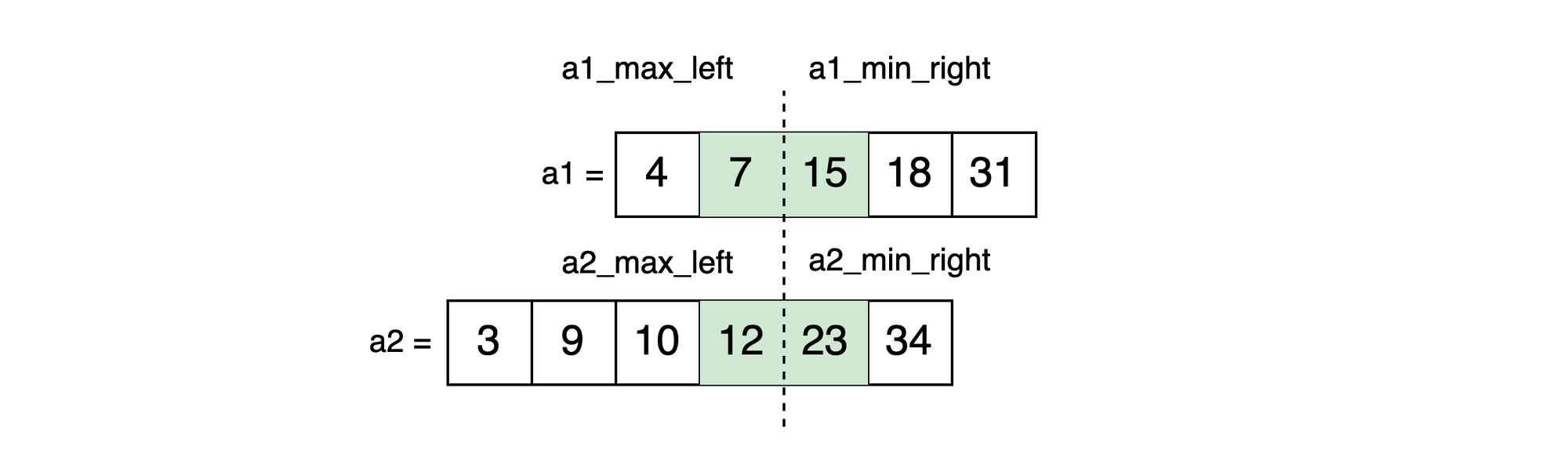
NOTE: When working with a single array with an odd number of elements, we can take the center element to find the median.

Finding the median for two arrays, works the same way.  When the total number of elements combined is odd, we take a single value:  max of both left values.

cond do
  a1_max_left <= a2_min_right and a2_max_left <= a1_min_right ->
    max_left = max(a1_max_left, a2_max_left)
    min_right = min(a1_min_right, a2_min_right)

    if Integer.mod(m + n, 2) == 0 do
      (max_left + min_right) / 2
    else
      max_left
    end
    
  ...
end

Max of values on the left from both arrays: 12

Complexity Analysis

Glossing over the issue of having Linked Lists as inputs, let's imagine we started with :array data structures where count and get operations more efficient.

Constant Steps:

1. Finding shortest array: ~3 steps
2. Set intital range: 1 step

Total: 4

Recursive Steps R (per array):

1. Partitioning arrays: 2 steps
2. Assigning left/right, min/max values: 4 steps
3. Checking conditions: ~5 steps

Total: R * 11 + 4

x is the length of the shortest array, R is the number of recursive iterations:

x    | R   | steps
-----------------------
100  | 7   | 81
200  | 8   | 92
400  | 9   | 103

To graph the differences between Linear Search vs Binary Search:

Because recursion has to re-partition both arrays, we can consider the time complexity: O(log(n+m)) and after dropping constants: O(log(n))

Wrapping Up

This was a much more complex problem than it seemed initially, but we covered a few important performance considerations such as Linear Search vs Binary Search and Linked Lists vs Arrays.

I'll likely cover a few more of these problems and solutions and then take deeper dives in Data Structures and Algorithms in Elixir.  

Thanks for reading and I hope you find these articles useful.

-- Troy

Twitter: @tmartin8080  | ElixirForum