LeetCode - Add Two Numbers | Elixir Solution

The second problem for LeetCode is called “Add Two Numbers”.  As the solutions become more complex, I’m noticing they’re harder to parse visually and am looking for ways to improve how they’re displayed.

For now, let’s squint together at some code and take our time reading through the details ;)

Add Two Numbers - Problem

You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order, and each of their nodes contains a single digit.

Add the two numbers and return the sum as a linked list.

You may assume the two numbers do not contain any leading zero, except the number 0 itself.

Example 1

Input: l1 = [2,4,3], l2 = [5,6,4]
Output: [7,0,8]
Explanation: 342 + 465 = 807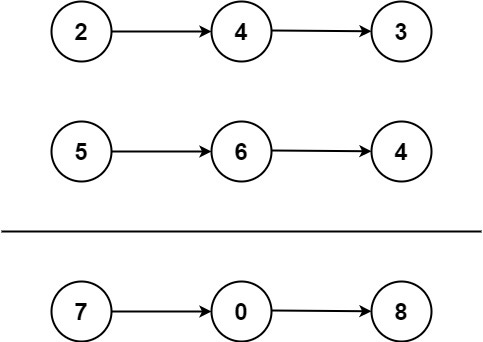

Example 2

Input: l1 = [0], l2 = [0]
Output: [0]

Example 3

Input: l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
Output: [8,9,9,9,0,0,0,1]

Constraints:

• The number of nodes in each linked list is in the range [1, 100].
• 0 <= Node.val <= 9
• It is guaranteed that the list represents a number that does not have leading zeros.

Solution

add_two_numbers/2 expects linked list struct ListNode or nil as arguments and return value.

Here is the ListNode struct:

defmodule ListNode do
  @type t :: %__MODULE__{
          val: integer,
          next: ListNode.t() | nil
        }
  defstruct val: 0, next: nil
end

Each node has a value and a link to the next node.

defmodule Solution do
  def add_two_numbers(l1, l2) do
    total = 0 
    exponent = 1
    value1 = list_to_integer(l1, total, exponent)
    value2 = list_to_integer(l2, total, exponent)

    (value1 + value2)
    |> Integer.digits()
    |> Enum.reverse()
    |> to_linked_list()
  end

  defp list_to_integer(nil, total, _), do: total

  defp list_to_integer(node, total, exponent) do
    %ListNode{val: current_value, next: next_node} = node
    new_total = total + current_value * exponent
    new_exponent = exponent * 10
    list_to_integer(next_node, new_total, new_exponent)
  end

  defp to_linked_list([]), do: nil

  defp to_linked_list([h | tail]) do
    %ListNode{val: h, next: to_linked_list(tail)}
  end
end

TLDR;

The incoming linked lists are the individual digits of a larger number and they are already reversed.  We can iterate over each list, accumulate the total value and increase the power of 10.

Then split the resulting total using Integer.digits/1, reverse the order and rebuild the values into a Linked List.

Time Complexity: O(max(m,n))

Source: https://github.com/tmartin8080/leet

---

Approach - Explanation

To begin, the data structure we’re working with is a Linked List. Essentially, a Linked List is a list of nodes that each know the location in memory of the next node:

[2, 4, 5]

# becomes:

%ListNode{
  val: 2
  next: %ListNode{
    val: 4,
    next: %ListNode{
      val: 3,
      next: nil
    }
  }
}

(I’ll some more detailed writing on Data Structures soon, but let’s continue for now.)

Given our values are represented as a reversed, linked-list we’d want to first convert the linked lists to an integer value:

[2, 4, 5] -> 542

Linked List to Integer

To accomplish this, we set initial values for total and exponent and pass them into a recursive function that is invoked for both linked lists:

total = 0 
exponent = 1
value1 = list_to_integer(l1, total, exponent)
value2 = list_to_integer(l2, total, exponent)

For the recursive function, we identify the base case:

When the current node’s value is nil we’ve reached the end of the Linked List

defp list_to_integer(nil, total, _), do: total

To handle all other cases:

defp list_to_integer(node, total, exponent) do
  %ListNode{val: current_value, next: next_node} = node
  new_total = total + current_value * exponent
  new_exponent = exponent * 10
  list_to_integer(next_node, new_total, new_exponent)
end

Let’s walk through this function using [2, 4, 5] as an example:

First Iteration:

# total = 0, exponent = 1
%ListNode{val: 2, next: %ListNode{val: 4, ...}} = node

new_total = 0 + 2 * 1 (2)
new_exponent = 1 * 10 (10)

The function then calls itself with updated values:

list_to_integer(%ListNode{val: 4, ...}, 2, 10)

Second Iteration

# total = 2, exponent = 10
%ListNode{val: 4, next: %ListNode{val: 5, ...}} = node

new_total = 2 + 4 * 10 = 42
new_exponent = 10 * 10 = 100

Again calling itself with updated values:

list_to_integer(%ListNode{val: 5, ...}, 42, 100)

Third Iteration

# total = 42, exponent = 100
%ListNode{val: 5, next: nil} = node

new_total = 42 + 5 * 100 = 542
new_exponent = 100 * 10 = 1000

Again, the function calls itself with updated values:

Notice: the next value is nil

list_to_integer(nil, 542, 100)

This will be handled by the base case function head:

defp list_to_integer(nil, 542, _), do: 542

Which simple drops our exponent temp variable and returns the value as an integer.

Sum Integers

After converting both linked lists to integers, we can sum them:

(value1 + value2)

Because our problem requires a reversed Linked List that represents an integer value, we need to convert the sum value to a Linked List.

Integer to Linked List

First, we convert the integer to an Elixir list and reverse it:

> Integer.digits(542)
[5, 4, 2]

> List.reverse([5, 4, 2])
[2, 4, 5]

Then call another recursive function that builds the ListNode struct.  Our base case would be:

When the list is empty there are no more nodes to link

defp to_linked_list([]), do: nil

Otherwise, separate the head of the list from the tail and build the current node:

# h = 2, tail = [4, 5]
defp to_linked_list([h | tail]) do
  %ListNode{val: h, next: to_linked_list(tail)}
end

This function calls itself to build the next node using the tail values.

Complexity Analysis

Given that we have two lists as arguments we can assign their respective sizes to M and N.

We’ll also assign the size of the returned sum integer: X

1. Converting both Linked Lists to integers: (2 steps * M) + (2 steps * N)
2. Sum of Integers: 1 step
3. Split integer: 1 step
4. Reverse integer: X steps
5. Convert integer to Linked List: X steps

Approx Steps:

M   | N   | X   | steps
-----------------------
1   | 1   | 1   | 8
10  | 10  | ~10 | ~70
100 | 100 | ~100 | ~700

X is dependant on the max of M or N

As M or N increase, total steps increase linearly depending on the max of either size.

By dropping constants and taking the worse-case scenario, we can say this algorithm is:

O(max(M, N))

Wrapping up

I’m currently working through different resources on Big O Notation and how to analyze Elixir data structures and algorithms.  This is obviously a broad subject so if you find any issues with the ideas or have ways to improve them, feel free to contact me.

Hope you enjoyed this article.

If you have comments or feedback, feel free to hit me up on Twitter: https://twitter.com/tmartin8080

Happy coding!

-- Troy